- Що таке діаметр кола
- Визначення діаметра кола
- Формула обчислення діаметра
- Історичні аспекти
- Властивості діаметра
- Основні властивості
- Теоретичні основи
- Взаємозв’язок з іншими елементами кола
- Радіус і діаметр
- Обчислення довжини кола
- Область кола
- Таблиця розрахунків: діаметр, радіус, довжина кола і площа
- Застосування діаметра у різних галузях
- Інженерія і будівництво
- Комп’ютерна графіка
- Наука і технології
- Висновок
Що таке діаметр кола
Що таке діаметр кола? Це питання може здатися простим, але воно є фундаментальним для розуміння геометрії кола в математиці. Діаметр кола є однією з найважливіших характеристик даної геометричної фігури. У цій статті ми детально розглянемо, що таке діаметр кола, його властивості, застосування та значення в різних галузях. Ми дослідимо історичні аспекти, розглянемо взаємозв’язок з іншими елементами кола, а також застосування діаметра в науці та техніці.
Визначення діаметра кола
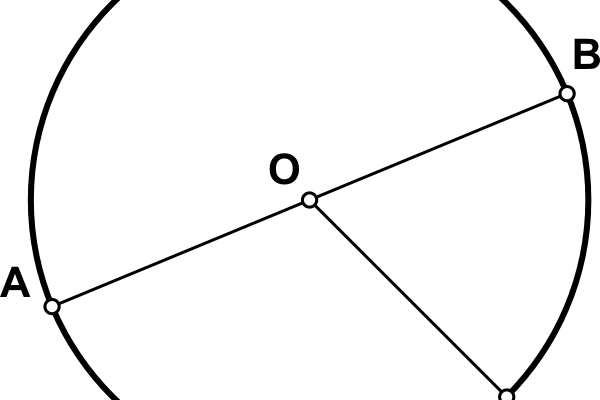
Діаметр кола — це відстань між двома найвіддаленішими точками кола, що проходять через центр кола. Він представляє собою пряму лінію, яка проходить через центр кола, починається на одній з точок кола і закінчується на протилежній точці кола. Діаметр є найбільшою можливою відстанню між двома точками кола.
Формула обчислення діаметра
Діаметр кола зазвичай позначається символом d. Формула для обчислення діаметра через радіус виглядає так:
- d = 2r
Де r — радіус кола. Іншими словами, діаметр дорівнює подвоєному радіусу.
Історичні аспекти
Історія вивчення кола бере свій початок ще з давніх часів. Відомо, що кола й діаметри використовувалися у стародавніх цивілізаціях, таких як єгиптяни та вавилоняни, для різних інженерних задач та вимірювань. У праці Евкліда «Начала», яка стала основою для геометрії, діаметр відіграє ключову роль у поясненні властивостей кола та геометричних рисунках.
Властивості діаметра
Основні властивості
- Діаметр завжди проходить через центр кола.
- Діаметр ділить коло на дві рівні частини, тобто на дві півкола.
- Довжина діаметра є подвоєною довжиною радіуса.
- Діаметр є найдовшою хордою кола.
Теоретичні основи
З точки зору теорії, діаметр є наочним прикладом використання простих властивостей геометрії для опису складних об’єктів. Він є основою багатьох геометричних теорем і доведень, наприклад, теореми про рівновіддаленість точок на колі відносно центру.
Взаємозв’язок з іншими елементами кола
Радіус і діаметр
Одним з ключових елементів при розгляді кола є його радіус. Що таке діаметр кола без врахування радіуса? Це всього лише подвоєний радіус, що відображає взаємозв’язок між цими величинами.
Обчислення довжини кола
Довжина кола C може бути обчислена за допомогою діаметра через формулу:
- C = πd
Де π — це константа, яка приблизно дорівнює 3,14159.
Область кола
Область кола A також може бути пов’язана із діаметром:
- A = (πd²)/4
Ця формула показує, як діаметр впливає на площу круглої фігури.
Таблиця розрахунків: діаметр, радіус, довжина кола і площа
| Параметр | Формула | Пояснення |
|---|---|---|
| Діаметр (d) | d = 2r | Діаметр в два рази більший за радіус |
| Радіус (r) | r = d/2 | Радіус дорівнює половині діаметра |
| Довжина кола (C) | C = πd | Довжина залежить лінійно від діаметра |
| Площа кола (A) | A = (πd²)/4 | Площа залежить квадратично від діаметра |
Застосування діаметра у різних галузях
Інженерія і будівництво
У галузі інженерії та будівництва визначення та точне вимірювання діаметра є критично важливими. Це важливо для створення креслень, розробки механічних частин, а також для побудови різноманітних конструкцій, де важлива симетрія та точність.
Комп’ютерна графіка
У комп’ютерній графіці поняття діаметра використовується для рендерингу круглих об’єктів та у алгоритмах, які передбачають симетрію та масштаби.
Наука і технології
Діаметр грає значну роль в астрономії при обчисленні розмірів небесних тіл і їх орбітальних параметрів. У біології діаметри клітин і судин є важливими характеристиками, що впливають на їх функціонування.
Висновок
Отже, що таке діаметр кола? Це базова характеристика кола, яка має багато застосувань у різних галузях науки і техніки. Від розрахунку довжини та площі кола до складних наукових досліджень — поняття діаметра відіграє ключову роль і залишається незамінним інструментом у роботі інженерів, архітекторів, науковців та багатьох інших спеціалістів. Глибше розуміння цього простого, але настільки важливого параметра дозволяє не лише вирішувати складні задачі, але й сприяє розвитку технологій, створених людським розумом.