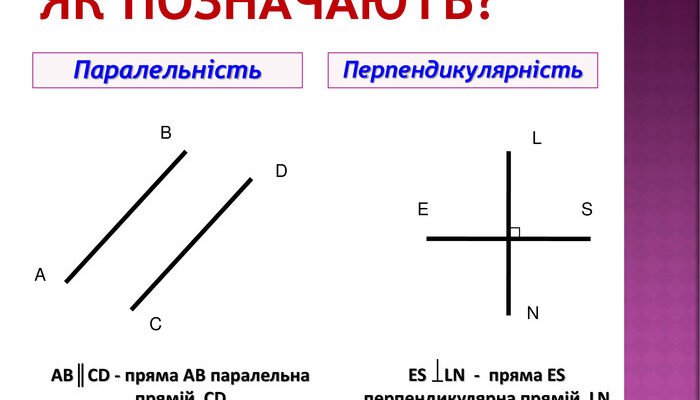
Що таке перпендикулярні прямі: пояснення простими словами

Що таке перпендикулярні прямі: визначення та геометричний зміст

Вступ до поняття перпендикулярності

Перш ніж зануритися в суть питання, що таке перпендикулярні прямі, слід визначити основні поняття, які відіграють ключову роль у геометрії. Перпендикулярні прямі є однією із фундаментальних складових геометричних теорій, які вивчають взаємодію просторових об’єктів.

Визначення перпендикулярних прямих

Перпендикулярні прямі — це дві прямі, які перетинаються на площині так, що формують чотири прямі кути, рівні між собою. Іншими словами, якщо дві прямі перетинаються та утворюють кут в 90 градусів, то такі прямі називають перпендикулярними. Кожен з кутів, утворених при перетині перпендикулярних прямих, є прямим кутом.

Геометричний зміст перпендикулярності

Перпендикулярність має важливе значення у багатьох галузях, включаючи архітектуру, дизайн, інженерію і навіть у природу. Вона дозволяє обчислити відстані, створити правильні форми і структури. У математиці перпендикулярність важлива, оскільки вона забезпечує основи для тригонометричних функцій, таких як синус і косинус, які необхідні для розв’язування задач різних рівнів складності.

Властивості перпендикулярних прямих

Основні властивості

• Прямі кути: Кути, утворені перетином перпендикулярних прямих, завжди є прямими.
• Взаємний вплив: Перпендикулярність є взаємним явищем: якщо пряма a перпендикулярна до прямої b, то й b перпендикулярна до a.
• Мітки на кресленнях: Перпендикулярні прямі часто позначаються квадратами на кресленнях, що символізують прямі кути.

Застосування перпендикулярності у практиці

Перпендикулярні прямі використовуються в таких сферах, як картографія, будівництво та електроніка. Наприклад, перпендикулярні стіни забезпечують стійкість конструкції, а перпендикулярні лінії у схемах гарантують коректне функціонування електричних ланцюгів.

Перпендикулярність у координатній площині

Координати та рівняння

У координатній площині для двох перпендикулярних прямих із рівняннями вигляду y = k₁x + b₁ та y = k₂x + b₂, коефіцієнти k₁ і k₂ мають добуток, рівний -1, тобто:

Це вказує на те, що одна з прямих є оберненим відношенням нахилу іншої з протилежним знаком.

Векторна форма перпендикулярності

Перпендикулярність у векторному поданні виражається через скалярний добуток. Якщо вектори a і b є ортогональними, то їх скалярний добуток дорівнює нулю:

• a · b = 0

Історичний огляд розвитку концепції

Антична геометрія

Поняття перпендикулярності сходить до античності, що було викладено у трактатах Евкліда. Вони слугували основою для геометрії протягом багатьох століть, визначаючи точні правила для побудови та аналізу перпендикулярних елементів.

Сучасне застосування

У XX та XXI століттях, з розвитком технологій, концепція перпендикулярності стала ще важливішою. Вона знайшла застосування у комп’ютерному моделюванні, геодезії та багатьох інших напрямах, що потребують точності.

Як побудувати перпендикулярні прямі

Кроки для побудови

1. Виберіть пряму, до якої потрібно побудувати перпендикуляр.
2. Знайдіть точку на цій прямій, через яку пройде перпендикуляр.
3. Використовуйте транспортир або калькулятор для створення кута в 90 градусів.
4. Проведіть нову пряму через дану точку з кутом 90 градусів до першої.

Висновок

Розуміння того, що таке перпендикулярні прямі, є критично важливим для багатьох аспектів математики та практичного застосування у реальному світі. Перпендикулярність визначає не лише просторові взаємини між об’єктами, але й впливає на нашу здатність організовувати інформацію, виконувати точні розрахунки та дизайнерські рішення. Інтеграція принципу перпендикулярності забезпечує стабільність, точність та естетичність у багатьох сферах нашого життя.