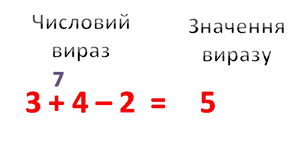Що таке вираз: Вступ до теми
Коли ми запитуємо себе, що таке вираз, ми звертаємось до основи математичних понять, які формують наше розуміння та вміння оперувати числами й символами. Вирази лежать в основі багатьох математичних дисциплін, від елементарної арифметики до вищої алгебри та аналізу, і тому важливо розібратися, що саме ми маємо на увазі під поняттям “вираз”.
Визначення та суть математичного виразу
Отже, що таке вираз? У найзагальнішому вигляді, математичний вираз представляє собою сукупність чисел, знаків математичних операцій, змінних та інших математичних символів, яка визначає певну величину. Особливістю виразів є те, що вони самостійно не мають конкретного значення, а лише описують спосіб його отримання при певних умовах або значеннях змінних.
Компоненти виразів
- Числа: Можуть бути цілими, дробовими або дійсними.
- Операції: До них належать додавання, віднімання, множення, ділення і т.д.
- Змінні: Літери, які представляють невідомі або змінні величини.
- Групування: Використання дужок для визначення порядку виконання операцій.
Типи виразів
Математичні вирази класифікуються за різними критеріями:
- Арифметичний вираз: Складається лише з чисел і операцій над ними. Приклад:
5 + 3 * 2 - Алгебраїчний вираз: Включає числа, змінні й операції. Приклад:
3x + 7 - Аналітичний вираз: Містить функції, такі як синус, косинус, логарифми тощо. Приклад:
sin(x) + ln(y)
Формулювання та обчислення виразів
Порядок дій у виразах
Щоб коректно обчислити значення виразу, важливо дотримуватись певних правил порядку дій:
| Операція | Порядок |
|---|---|
| Дії в дужках | 1 |
| Підносиення до степеня і корінь | 2 |
| Множення і ділення | 3 |
| Додавання та віднімання | 4 |
Наприклад, у виразі 2 + 3 * (4 - 2) слід спочатку виконати дію в дужках: 4 - 2 = 2, потім множення: 3 * 2 = 6, і нарешті додавання: 2 + 6 = 8.
Спрощення виразів
Часто робота з виразами передбачає їх спрощення. Це означає застосування правил алгебри для зведення виразу до простішого або компактнішого вигляду. Наприклад, вираз 2x + 3x можна спростити до 5x.
Вирази у різних галузях математики
Вирази в алгебрі
Алгебра – це розділ математики, де вирази грають ключову роль. Багато задач на обчислення або розв’язання рівнянь базуються на складних алгебраїчних виразах. Наприклад, квадратні рівняння, такі як ax^2 + bx + c = 0, є прикладами поліноміальних виразів, що містять змінні та константи.
Вирази в геометрії
У геометрії вирази часто використовуються для визначення довжин, площ, об’ємів та інших геометричних величин. Наприклад, для знаходження площі прямокутника використовується вираз l * w, де l – довжина, а w – ширина.
Вирази в аналізі
Аналіз використовує вирази для визначення границь, обчислення похідних та інтегралів. Вирази у цьому контексті можуть бути дуже складними і включати в себе функції від багатьох змінних.
Практичне застосування виразів
Ось деякі з повсякденних застосувань математичних виразів:
- Фінанси: Обчислення відсотків, відсоткових ставок, складних відсотків та інших фінансових показників.
- Комп’ютерні науки: Написання алгоритмів, програмування та вирішення різноманітних задач із використанням математичних виразів і логічних операторів.
- Фізика і інженерія: Моделювання фізичних процесів, обчислення траєкторій, сил, енергії тощо.
Заключні думки
Отже, підводячи підсумки, що таке вираз? Це фундаментальний елемент у математиці, що становить основу для багатьох областей наук і застосувань. Розуміння цього поняття є ключовим при вивченні математики та її застосуванні в реальному світі. Вирази допомагають нам не лише вирішувати складні математичні задачі, але й роблять зрозумілими та досяжними багато фізичних та економічних концепцій. За допомогою виразів ми можемо формалізувати нашу інтуїцію та знаходити рішення для численних проблем у різних сферах людської діяльності.